Localization

Example using several well doublets and compares ESMDA with and without localization.

The example follows contextually 2D Reservoir ESMDA example.

import numpy as np
import matplotlib.pyplot as plt

import dageo

# For reproducibility, we instantiate a random number generator with a fixed
# seed. For production, remove the seed!
rng = np.random.default_rng(2020)

Model parameters

# Grid extension
nx = 35
ny = 30
nc = nx*ny

# Permeabilities
perm_mean = 3.0
perm_min = 0.5
perm_max = 5.0

# ESMDA parameters
ne = 100                  # Number of ensembles
dt = np.zeros(10)+0.0001  # Time steps (could be irregular, e.g., increasing!)
time = np.r_[0, np.cumsum(dt)]

# Assumed sandard deviation of our data
dstd = 0.5

# Measurement points
ox = (5, 15, 24)
oy = (5, 10, 24)

# Number of data points
nd = time.size * len(ox)

# Wells
wells = np.array([
    [ox[0], oy[0], 180], [5, 12, 120],
    [ox[1], oy[1], 180], [20, 5, 120],
    [ox[2], oy[2], 180], [24, 17, 120]
])

Create permeability maps for ESMDA

We will create a set of permeability maps that will serve as our initial guess (prior). These maps are generated using a Gaussian random field and are constrained by certain statistical properties.

# Get the model and ne prior models
RP = dageo.RandomPermeability(nx, ny, perm_mean, perm_min, perm_max)
perm_true = RP(1, random=rng)
perm_prior = RP(ne, random=rng)

Run the prior models and the reference case

# Instantiate reservoir simulator
RS = dageo.Simulator(nx, ny, wells=wells)


def sim(x):
    """Custom fct to use exp(x), and specific dt & location."""
    return RS(np.exp(x), dt=dt, data=(ox, oy)).reshape((x.shape[0], -1))


# Simulate data for the prior and true fields
data_prior = sim(perm_prior)
data_true = sim(perm_true)
data_obs = rng.normal(data_true, dstd)
data_obs[0, :3] = data_true[0, :3]

Localization Matrix

# Vector of nd length with the well x and y position for each nd data point
nd_positions = np.tile(np.array([ox, oy]), time.size).T

# Create matrix
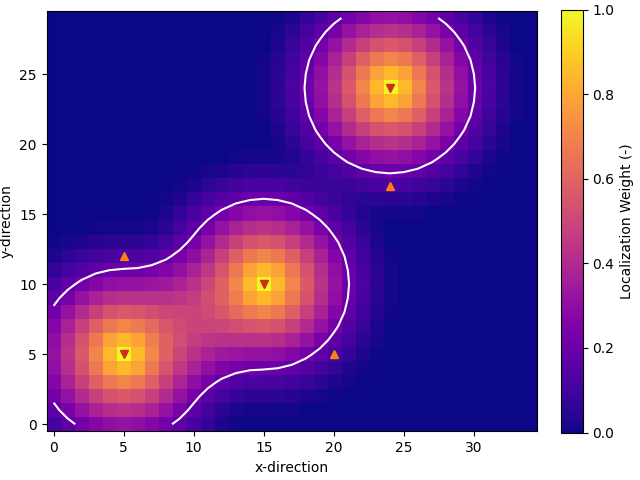
loc_mat = dageo.localization_matrix(RP.cov, nd_positions, (nx, ny))

# QC localization matrix
fig, ax = plt.subplots(1, 1, constrained_layout=True)
im = ax.imshow(loc_mat.sum(axis=2).T/time.size, origin='lower', cmap="plasma")
ax.contour(loc_mat.sum(axis=2).T/time.size, levels=[0.2, ], colors='w')
ax.set_xlabel('x-direction')
ax.set_ylabel('y-direction')
for well in wells:
    ax.plot(well[0], well[1], ['C3v', 'C1^'][int(well[2] == 120)])
fig.colorbar(im, ax=ax, label="Localization Weight (-)")

ESMDA

def restrict_permeability(x):
    """Restrict possible permeabilities."""
    np.clip(x, perm_min, perm_max, out=x)


inp = {
    'model_prior': perm_prior,
    'forward': sim,
    'data_obs': data_obs,
    'sigma': dstd,
    'alphas': 4,
    'data_prior': data_prior,
    'callback_post': restrict_permeability,
    'random': rng,
}

Without localization

nl_perm_post, nl_data_post = dageo.esmda(**inp)

ESMDA step   1; α=4.0
ESMDA step   2; α=4.0
ESMDA step   3; α=4.0
ESMDA step   4; α=4.0

With localization

wl_perm_post, wl_data_post = dageo.esmda(**inp, localization_matrix=loc_mat)

ESMDA step   1; α=4.0
ESMDA step   2; α=4.0
ESMDA step   3; α=4.0
ESMDA step   4; α=4.0

Compare permeabilities

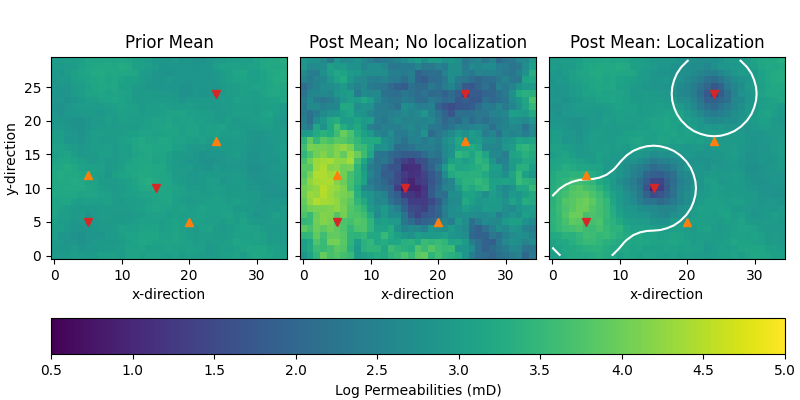
# Plot posterior
fig, axs = plt.subplots(
    1, 3, figsize=(8, 4), sharex=True, sharey=True, constrained_layout=True)

par = {"vmin": perm_min, "vmax": perm_max, "origin": "lower"}

axs[0].set_title("Prior Mean")
im = axs[0].imshow(perm_prior.mean(axis=0).T, **par)


axs[1].set_title("Post Mean; No localization")
axs[1].imshow(nl_perm_post.mean(axis=0).T, **par)

axs[2].set_title("Post Mean: Localization")
axs[2].imshow(wl_perm_post.mean(axis=0).T, **par)
axs[2].contour(loc_mat.sum(axis=2).T, levels=[2.0, ], colors="w")

fig.colorbar(im, ax=axs, label="Log Permeabilities (mD)",
             orientation="horizontal")

for ax in axs:
    for well in wells:
        ax.plot(well[0], well[1], ["C3v", "C1^"][int(well[2] == 120)])
for ax in axs:
    ax.set_xlabel('x-direction')
axs[0].set_ylabel('y-direction')

Compare data

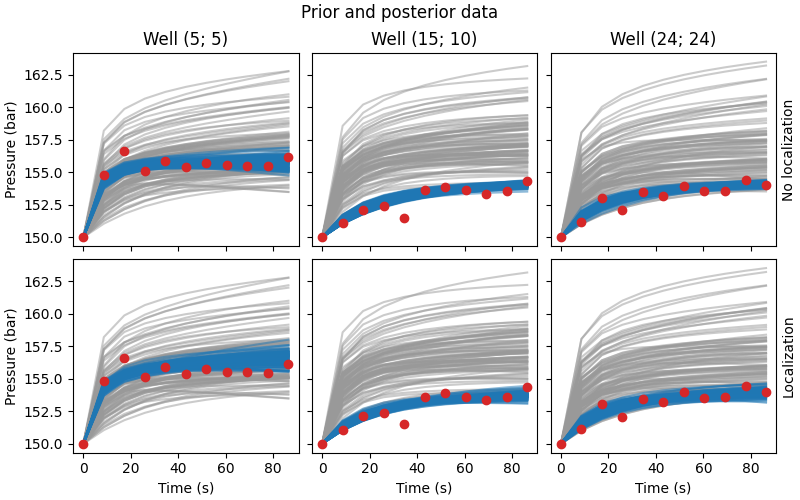
# QC data and priors
fig, axs = plt.subplots(
    2, 3, figsize=(8, 5), sharex=True, sharey=True, constrained_layout=True)
fig.suptitle('Prior and posterior data')
for i, ax in enumerate(axs[0, :]):
    ax.set_title(f"Well ({ox[i]}; {oy[i]})")
    ax.plot(time*24*60*60, data_prior[..., i::3].T, color='.6', alpha=0.5)
    ax.plot(time*24*60*60, nl_data_post[..., i::3].T, color='C0', alpha=0.5)
    ax.plot(time*24*60*60, data_obs[0, i::3], 'C3o')
for i, ax in enumerate(axs[1, :]):
    ax.plot(time*24*60*60, data_prior[..., i::3].T, color='.6', alpha=0.5)
    ax.plot(time*24*60*60, wl_data_post[..., i::3].T, color='C0', alpha=0.5)
    ax.plot(time*24*60*60, data_obs[0, i::3], 'C3o')
    ax.set_xlabel("Time (s)")
for i, ax in enumerate(axs[:, 0]):
    ax.set_ylabel("Pressure (bar)")
for i, txt in enumerate(["No l", "L"]):
    axs[i, 2].yaxis.set_label_position("right")
    axs[i, 2].set_ylabel(f"{txt}ocalization")

dageo.Report()

Fri Dec 06 15:59:20 2024 UTC
OS	Linux (Ubuntu 22.04)	CPU(s)	4	Machine	x86_64
Architecture	64bit	RAM	15.6 GiB	Environment	Python
File system	ext4
Python 3.12.7 (main, Oct 1 2024, 15:17:55) [GCC 11.4.0]
dageo	1.1.0	numpy	2.1.3	scipy	1.14.1
matplotlib	3.9.3	IPython	8.30.0

Estimated memory usage: 129 MB